Background
Many systems in engineering and science are modeled using variables that live on continuous domains (e.g., space-time), making them infinite-dimensional (i.e., variables are functions). Specific engineering applications include REE-CM supply chains, wildfire simulations, process systems, climate modeling, reaction surfaces, microbial communities, complex fluid flows, and molecular dynamics. My unifying abstraction (InfiniteOpt) enables simultaneous innovation across these areas. A common challenge pertains to complex systems which cannot be modeled from 1st principles and/or incur high computational cost.
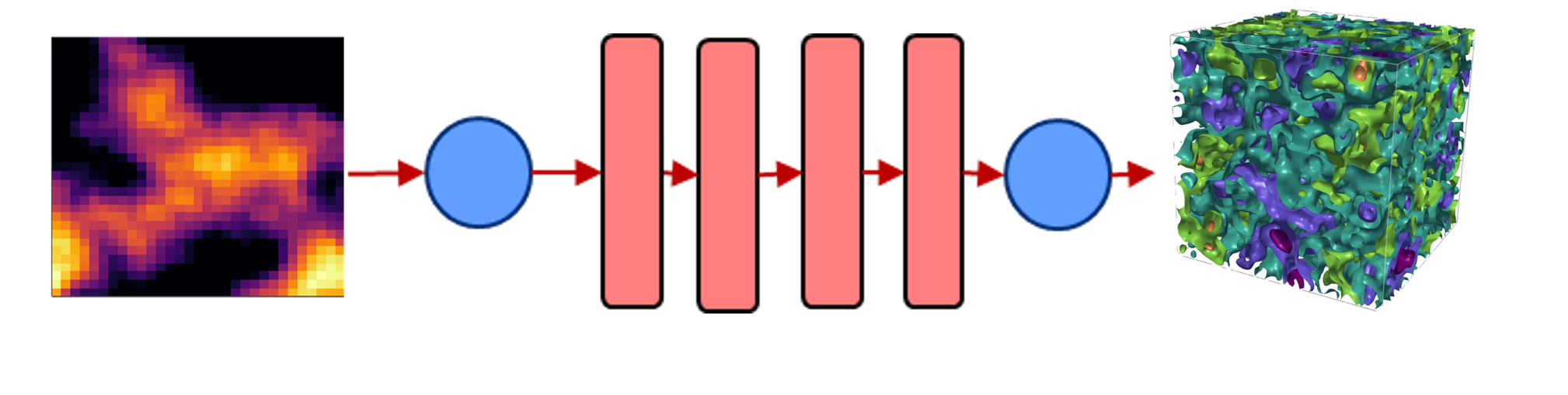
Nueral operators networks generalize popular neural networks to learn an operator that maps between functions instead of simply learning a single function. This has enabled neural operators to become the state-of-the-art in learning highly complex space-time systems (e.g., turbulent fluid flow). These highly effective models have gained a lot of traction in the machine learning community but have seen little use in mathematical programming.
Proposed Approaches
We propose to use neural operators as InfiniteOpt surrogates. To enable this, we will also engineer constraint representations of neural operators that embed in InfiniteOpt formulations. Taking inspiration from physics-informed neural network based control, we will also create a physics-informed decision-making framework that uses neural operators. Moreover, we plan to implement our scientific discoveries in \texttt{InfiniteOpt.jl</b> to promote accessibility and accelerate research in a wide breadth of disciplines.
